You live in year \(2050\) where hyperloop has been invented. Currently you are in city \(X\) and you want to reach city \(Y\) using minimum amount of money. From city \(u\) to \(v\) if you use hyperloop than it costs \(2\) dollars otherwise it costs \(1\) dollar.
Print the minimum cost to reach the end city from the starting city.
Input Format:
you are given \(N, M, K, start, end\) - the number of cities, number of roads and number of hyperloops, starting and ending city.
Next \(M\) line contains \(2\) values \(u\) and \(v\) meaning there is a bidirectional path between \(u\) and \(v\).
Next \(K\) lines contains \(2\) values \(u\) and \(v\) meaning there is a bidirectional hyperloop between city \(u\) and \(v\).
Output Format:
If it is impossible to reach the end city then print \(-1\)
Otherwise print the minimum cost to reach the end city from the starting city
Constraints:
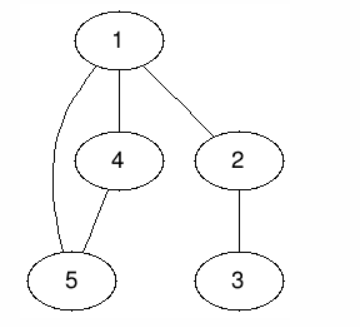
It can be clearly seen that if go through path 1 -> 2 -> 3.
It costs 3 dollars and for all other paths it costs more than 3 dollars.
Please login to use the editor
You need to be logged in to access the code editor
Loading...
Please wait while we load the editor
Login to unlock the editorial
Please login to use the editor
You need to be logged in to access the code editor
Loading...
Please wait while we load the editor