Given a \(3 * N\) matrix. In one operation you can swap any two-column and you can perform this operation any number of times (including zero). Find the minimum possible value of the given function after performing this operation any number of times (including zero). As this value may become very large, so output the answer modulo \(10^9 +7\). The function is given below:
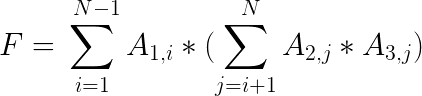
Input Format:
- The first line contains \(T\) denoting the number of test cases. The description of each test case is as follows.
- First-line contains an integer \(N\), denoting the number of columns of the matrix.
- It follows with \(3\) line each contains \(N\) integers.
Output Format:
- For each test case, print a single line containing one integer — the minimum value \(F\) modulo \(10^9 + 7\).
Constraints:
- \(1 \leq T \leq 15\)
- \(2 \leq N \leq 10^5\)
- \(1 \leq A_{1, i}, A_{2, i}, A_{3, i} \leq 10^4\)
We can swap 1'st and 2'nd column and the answer will be 2 * (1 * 20 + 2 * 2) + 1 * (2 * 2) = 52 and this the minimum possible answer.
Please login to use the editor
You need to be logged in to access the code editor
Loading...
Please wait while we load the editor
Login to unlock the editorial
Please login to use the editor
You need to be logged in to access the code editor
Loading...
Please wait while we load the editor